Section courante

A propos

Section administrative du site

Aviation

Dans le domaine de l'aviation moderne, l'informatique occupe une place de plus en plus centrale. Les avions d'aujourd'hui intègrent une multitude de capteurs («sensors») fournissant aux pilotes des informations en temps réel, cruciales pour la sécurité et la précision des vols. Dans le cockpit, chaque milliseconde compte : les calculs ne se font pas en simple délai temporel, mais souvent en Hertz, pour mesurer la fréquence à laquelle un processus doit s'exécuter.

Les capteurs

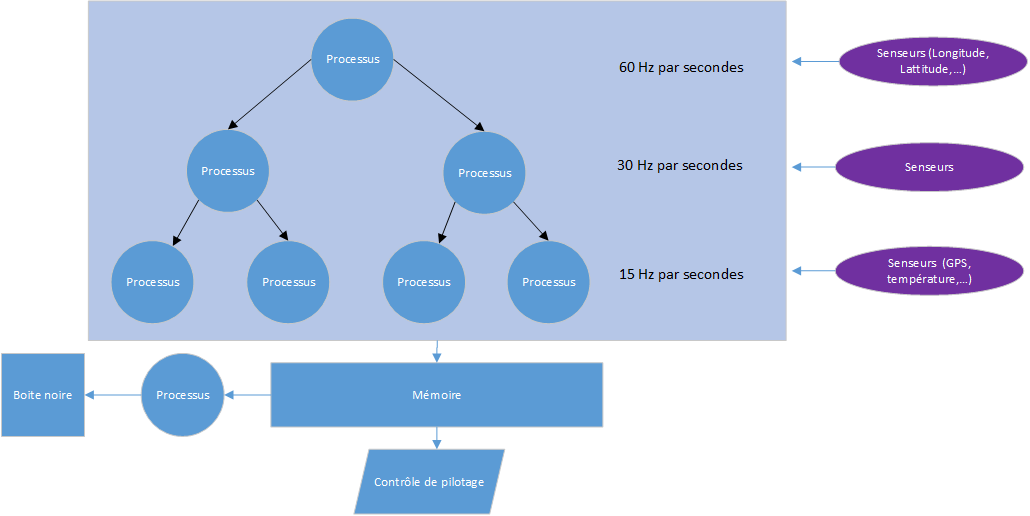
Parmi les composantes faisant place à bord de l'appareil, se trouve maintenant des senseurs utiliser pour fournir des informations en temps réels aux pilotes des avions. Et quand on parle de temps réel, c'est d'autant plus vrai dans le cockpit d'un avion ! Ainsi, par exemple, on calcul le nombre de temps que prendra un processus en Hertz plutôt qu'un délai en millisecondes. Et tout les processus non pas le même niveau de priorité et de fréquence, ainsi, les senseurs de la longitude et la latitude on une fréquence beaucoup plus élevé que les senseurs retournant les informations du GPS ou de la température. Les processus doivent avoir un délai extrêmement court car sinon, il pourrait induire le pilote en erreur et causer un écrasement. Ainsi, par exemple, pour obtenir un délai optimale, les processus effectuent des écritures directement dans une mémoire partagé afin d'éviter d'effectuer des traitements inutile. Ainsi, on préféra la programmation en langage de programmation Ada ou C plutôt qu'en C++ pour éviter les lourdeurs de traitements de mémoire de la programmation orienté objet (POO) n'ayant pas sa place dans un engin où la sécurité des passagers est primordiale. Aussi, les unités de mesures utilisés pour obtenir les coordonnée de l'appareil sont calculé en mille nautique plutôt que Kilomètre ou en Mille, soit 1 mille nautique = 1,852 Kilomètre, afin d'avoir exactement 1/20e de degré de latitude et ainsi avoir une correspondance plus adéquates à la planète terre.

Calcul du centre de gravité

Le centre de gravité d'un avion est l'un des paramètres les plus critiques pour assurer sa stabilité et sa sécurité en vol. Il correspond au point d'application de la résultante de toutes les forces de gravité agissant sur l'appareil, et sa position doit rester dans des limites strictes définies par le constructeur. Un centre de gravité mal calculé peut compromettre la manouvrabilité de l'avion et même provoquer des situations dangereuses, telles que des décrochages ou des pertes de contrôle.

Le calcul du centre de gravité repose sur la mesure précise de la masse et de la position de chaque composant de l'avion : carburant, passagers, bagages, cargaison, moteurs et autres équipements. Chaque élément est considéré comme un point de masse dont la position est connue dans un repère tridimensionnel. Le centre de gravité total est alors obtenu par la formule classique de la moyenne pondérée :

Xcg=∑(mi×xi)/∑mi,Ycg=∑(mi×yi)/∑mi,Zcg=∑(mi×zi)/∑mi

où mi est la masse de l'élément i, et xi,yi,zi ses coordonnées.

Voici un petit exemple de code Turbo Pascal illustrant le calcul du centre de gravité pour un avion avec trois masses :

  1. Program CentreDeGravite;
  2. Type
  3.  TPoint=Record
  4.   x,y,z:Real;
  5.   masse:Real;
  6.  End;
  7. Var
  8.  points:Array[1..3] of TPoint;
  9.  i:Integer;
  10.  Xcg,Ycg,Zcg,masseTotale:Real;
  11. Begin
  12.   { Définition des masses et positions }
  13.  points[1].x := 5; points[1].y := 2; points[1].z := 1; points[1].masse := 1000;
  14.  points[2].x := 10; points[2].y := 3; points[2].z := 2; points[2].masse := 1500;
  15.  points[3].x := 15; points[3].y := 5; points[3].z := 3; points[3].masse := 1200;
  16.  Xcg:=0; Ycg:=0; Zcg:=0; masseTotale:=0;
  17.  For i:=1 to 3 do Begin
  18.    Xcg := Xcg + points[i].x * points[i].masse;
  19.    Ycg := Ycg + points[i].y * points[i].masse;
  20.    Zcg := Zcg + points[i].z * points[i].masse;
  21.    masseTotale := masseTotale + points[i].masse;
  22.  End;
  23.  Xcg := Xcg / masseTotale;
  24.  Ycg := Ycg / masseTotale;
  25.  Zcg := Zcg / masseTotale;
  26.  Writeln('Centre de gravité (X, Y, Z) = ', Xcg:0:2, ', ', Ycg:0:2, ', ', Zcg:0:2);
  27. END.

Dans cet exemple : Chaque point correspond à un élément avec sa masse et ses coordonnées, la boucle for calcule la somme pondérée des positions et on divise ensuite par la masse totale pour obtenir le centre de gravité exact.

Dans les avions modernes, ce calcul n'est plus seulement effectué manuellement. Les systèmes informatiques embarqués utilisent des processus temps réel pour suivre les variations de masse, par exemple lors de la consommation de carburant ou du déplacement de la cargaison. Ces calculs doivent être extrêmement rapides et fiables : une mise à jour toutes les quelques secondes est souvent nécessaire pour fournir aux pilotes des informations exactes et leur permettre d'ajuster leur plan de vol si besoin.

Comme pour les autres systèmes critiques, le choix du langage de programmation est important. Des langages efficaces et sûrs comme Ada ou C sont utilisés pour minimiser les risques d'erreurs et garantir que les calculs se déroulent sans surcharge inutile. Les résultats sont souvent stockés dans des mémoire partagée ou envoyés directement aux instruments de bord, pour éviter toute latence pouvant nuire à la sécurité.

Enfin, les unités utilisées dans le calcul du centre de gravité sont adaptées aux standards aéronautiques. Les distances sont exprimées en milles nautiques et les masses en kilogrammes, assurant une compatibilité avec tous les instruments et cartes de navigation. La précision est telle que le déplacement d'un seul passager peut être pris en compte dans la réévaluation du centre de gravité, garantissant une stabilité optimale tout au long du vol.



Dernière mise à jour : Jeudi, le 26 décembre 2019